Esta
onda é um elétron!
A
Mecânica Ondulatória é um ramo da Física
que estuda a dupla natureza da matéria – ondulatória
e corpuscular. Ou seja: estuda as diversas formas de onda existentes,
como, por exemplo, o som, a luz, as ondas do mar e qualquer outro
fenômeno oscilatório, demonstrando suas formas de propagação,
absorção e propriedades. Onda é qualquer e
toda perturbação que se propaga. Há dois tipos
básicos de ondas: mecânicas (som) e eletromagnéticas
(luz).
A
dualidade partícula-onda foi enunciada pela primeira vez
em 1924 pelo físico francês Louis-Victor de Broglie
(1892 – 1987), que concluiu que os elétrons apresentavam
características tanto ondulatórias como corpusculares
(estendendo o caráter dual da luz para a matéria),
isto é, o elétron se comporta de um ou outro modo
– luz ou matéria – a depender do experimento
específico a que esteja submetido.
Em
resumo, o Princípio de Louis de Broglie atribui um comprimento
de onda de matéria para qualquer massa m
com velocidade v. Na relação abaixo,
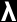é o comprimento
de onda, h é a constante de Planck e p
= mv é o produto da massa (m) pela
velocidade (v) da partícula (o momento linear
da partícula).
Isto
nos obriga a considerar o Princípio da Incerteza de Werner
Karl Heisenberg (1901 – 1976), que impõe restrições
à precisão com que se podem efetuar medidas simultâneas
em uma classe de pares de observáveis, como, no caso, a posição
e a velocidade de um elétron. Pode-se exprimir o Princípio
da Incerteza nos seguintes termos: O
produto da incerteza associada ao valor de uma coordenada x
(
)
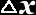e a incerteza associada ao seu correspondente momento linear p
(
)
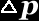não pode ser inferior, em grandeza, à Constante de
Planck normalizada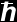 
(Constante de Plank – 
–
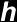dividida por 2 
).
Em outras palavras: não é possível, com precisão,
determinar simultaneamente a velocidade e a posição
de um elétron em um determinado átomo. Na verdade,
é possível especificar a posição ou
a velocidade do elétron de modo isolado, mas, à medida
que se aumenta, por exemplo, a precisão na determinação
da posição, perde-se a precisão na determinação
da velocidade. Isto significa que quanto maior for a precisão
da medida da posição de um elétron no átomo,
menos precisa será a determinação de sua velocidade
de movimentação e vice-versa. Em termos matemáticos,
este conceito se exprime assim:
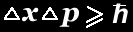
Tudo
está associado, interligado; a incerteza e a imprecisão
são nossas.
Fontes:
http://www.brasilescola.com/quimica/
o-principio-incerteza-heisenberg.htm
http://www.collectionscanada
http://pt.wikipedia.org/wiki/Princ%C3%
ADpio_da_incerteza_de_Heisenberg
http://lief.if.ufrgs.br/~jader/deBroglie.pdf
http://pt.wikipedia.org/wiki/Dualidade
_onda-corp%C3%BAsculo
http://pt.wikipedia.org/wiki/Mec%
C3%A2nica_ondulat%C3%B3ria