Rodolfo Domenico Pizzinga

 

 

 

Introdução e Objetivo do Estudo

 

 

 

Arquitas de Tarento

 

 

Arquitas de Tarento (428 a.C. – 347 a.C.), filósofo e cientista grego, é considerado o mais ilustre dos matemáticos pitagóricos. Acredita-se ter sido discípulo de Filolau de Crotona (século V a.C.) e foi contemporâneo de Platão (428/427 – Atenas, 348/347 a.C.). Fundou a mecânica e influenciou Euclides de Alexandria (360 a.C. – 295 a.C.). Foi o primeiro a usar o cubo em Geometria e a restringir a Matemática às disciplinas técnicas como a Geometria, a Aritmética, a Astronomia e a Acústica. Para resolver o famoso problema da duplicação do cubo (um dos três problemas clássicos da Antigüidade), Arquitas se valeu de um modelo tridimensional (determinando um certo ponto como a intersecção de três superfícies de revolução, como explica Thomas Little Heath, 1861 – 1940, na sua A History of Greek Mathematics I). Os gregos, todavia, estavam familiarizados com um problema semelhante, porém, bem mais simples: duplicar o quadrado.¹

 

Embora inúmeras obras sobre mecânica e geometria lhe sejam atribuídas, restaram apenas fragmentos, cuja preocupação central é a Matemática e a Música.

 

Arquitas também atuou na política. Os tarentinos o elegeram estratego (governador) sete vezes consecutivas.

 

Morreu em um naufrágio na costa de Apúlia – uma região da Itália meridional.

 

Este estudo teve por objetivo recolher os poucos fragmentos que chegaram até nós, que, nomeadamente, tratam de problemas de Matemática e de Música.

Geometria, Aritmética e Música parecem ser ciências irmanadas, pois se ocupam das duas formas primeiras e emparelhadas dos seres: número e grandeza.

 

Um choque só surgirá quando corpos em movimento se encontrarem vindos de lados opostos, e se baterem.

 

 

 

 

Os ruídos muito fortes não podem penetrar em nosso ouvido, como também nos vasilhames de boca estreita nada se consegue derramar, quando se quer derramar muito.

 

Os ruídos que conseguem penetrar em nossos sentidos nos parecem agudos quando o choque vem a nós rápida e fortemente, e graves quando lenta e fracamente.

 

Um tom produzido com respiração forte soará com força e de modo agudo; mas, se a respiração for fraca, soará de modo débil e grave.

 

O movimento rápido produz um som agudo eo lento um som grave.

 

Há três proporções na música: a aritmética, a geométrica e a contraposta, chamada harmonia. A aritmética se dá quando três termos manifestam analogicamente a seguinte diferença: o segundo supera tanto o primeiro quanto o terceiro supera o segundo. Nesta analogia, se vê que a relação dos termos maiores é menor e a dos menores é maior. A geométrica ocorre quando o primeiro termo está para o segundo assim como o segundo está para o terceiro. As maiores guardam a mesma relação que as menores. A contraposta, também chamada proporção harmônica, é produzida quando os termos se comportam da seguinte maneira: Quando, da própria grandeza, o primeiro termo supera o segundo tanto quanto o médio supera o terceiro. Nesta analogia, a relação dos termos maiores é maior; já a dos menores é menor.

 

Deve-se chegar ao conhecimento daquilo que se ignora aprendendo de um outro ou por pesquisa própria. Aquele que nada entende de investigação nada poderá encontrar.

 

Quando se consegue encontrar a razão, esta aumenta a concórdia fazendo cessar a rebelião. Pela razão, poderemos nos reconciliar.

 

Os injustos que sabem raciocinar desistem da injustiça antes de a cometerem, convencendo-se de que não poderão ficar ocultos quando voltarem ao mesmo lugar.²

 

A Aritmética tem predominância sobre as outras ciências por poder demonstrar claramente o que quer.³

 

 

 

______

Notas:

1. A duplicação do cubo é um problema de Geometria que consiste em obter um método para, dada a aresta de um cubo, construir, com régua e compasso, a aresta do cubo cujo volume é o dobro do cubo inicial. Era do conhecimento dos pitagóricos que, dado um quadrado, era possível construir um novo quadrado com o dobro de sua área. Tal problema é relatado por Platão em um dos seus diálogos, Menon, que trata do ensino da virtude. Neste diálogo, Sócrates é retratado ensinando um jovem e inculto escravo a duplicar um quadrado. Trecho do diálogo:

Sócrates: — Examina, agora, o que em seguida a estas dúvidas ele irá descobrir, procurando comigo. Só lhe farei perguntas; não lhe ensinarei nada! Observa bem se o que faço é ensinar e transmitir conhecimentos ou se é apenas perguntar ao interlocutor o que ele sabe. Responde-me: não é esta a figura de nosso quadrado, cuja área mede quatro pés quadrados?

Escravo: — É.

Sócrates: — A este quadrado não poderemos acrescentar este outro, igual?

Escravo: — Podemos.

Sócrates: — Que múltiplo do primeiro quadrado é a grande figura inteira?

Escravo: — O quádruplo.

Sócrates: — E devíamos obter o dobro, recordaste?

Escravo: — Sim.

Sócrates: — E esta linha, traçada de um vértice a outro de cada um dos quadrados interiores, não divide ao meio a área de cada um deles?

Escravo: — Divide.

Sócrates: — E não temos, assim, quatro linhas que constituem uma figura interior?

Escravo: — Exatamente.

Sócrates: — Repara, agora. Qual é a área desta figura?

Escravo: — Não sei.

Sócrates: — Mas, não dissemos que cada linha, nestes quatro quadrados, dividia cada um pela metade?

Escravo: — Sim, dissemos.

Sócrates: — Bem, então, quantas metades temos aqui?

Escravo: — Quatro.

Sócrates: — E aqui?

Escravo: — Duas.

Sócrates: — E em que relação aquelas quatro estão para estas duas?

Escravo: — O dobro.

Sócrates: — Logo, quantos pés quadrados mede esta superfície?

Escravo: — Oito.

Sócrates: — E qual é seu lado?

Escravo: — Esta linha.

Sócrates: — A linha traçada no quadrado de quatro pés quadrados, de um vértice a outro?

Escravo: — Sim.

Sócrates: — Os sofistas dão a esta linha o nome de diagonal e, por isto, usando este nome, podemos dizer que a diagonal é o lado de um quadrado de área dupla, exatamente como tu, ó escravo de Menon, o afirmaste.

Escravo: — Exatamente, Sócrates!

Duplicação do quadrado: dado um quadrado ABCD, traçar a sua diagonal BD e construir um quadrado de lado BD. É fácil perceber que BDEF tem o dobro da área de ABCD. Assim, dado um quadrado de lado a é possível encontrar um outro quadrado de lado b cuja área seja o dobro da área do primeiro, portanto (onde b é a diagonal do quadrado original).

 

 

 

2. Ora, isto não é mesmo assim. E, se fosse, seria meramente uma decisão hipotética, destituída de qualquer valor espiritual. Misticamente, só devemos agir por imperativos categóricos. Imperativo categórico é um dos principais elementos da Filosofia de Immanuel Kant (1724 – 1804). Sua Ética e Moral têm como base este preceito. Para o filósofo alemão, imperativo categórico é o dever de toda pessoa agir conforme os princípios que ela quer que todos os seres humanos sigam; que ela quer, enfim, que seja uma Lei da Natureza. O imperativo categórico pode ser enunciado de três formas diferentes. São elas: 1ª) Age como se a máxima de tua ação devesse se tornar, por tua vontade, Lei Universal da Natureza; 2ª) A máxima do meu agir deve ser por mim entendida como uma Lei Universal; e 3ª) Age de tal modo que possas usar a Humanidade, tanto em tua pessoa como na pessoa de qualquer outro, sempre como um fim ao mesmo tempo, e nunca apenas como um meio. Isto é difícil? É; mas devemos nos esforçar para sempre agir assim por pensamentos, palavras e atos. Portanto, não há abominação maior do que (tentar) fazer negócios com Deus.

3. O Teorema das Quatro Cores é um teorema de formulação e conceitualização muito simples, mas de demonstração extremamente complexa, pois só pode ser demonstrado com o auxílio de um computador. A sua formulação é a seguinte: Dado um mapa plano, dividido em regiões, quatro cores são suficientes para colori-lo, de forma a que regiões vizinhas não compartilhem a mesma cor. Regiões que só se tocam em um ponto não são consideradas vizinhas. Seguindo a proposição do Teorema das Quatro Cores, tente colorir o pretenso contra-exemplo abaixo do matemático Martin Gardner (1914 – 2010). A resposta está logo abaixo.

 

 

 

 

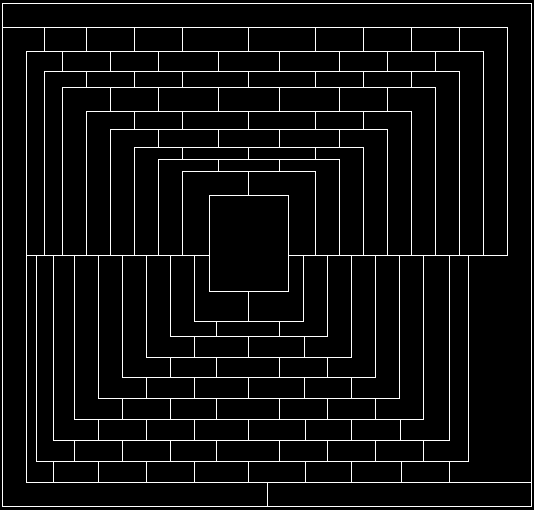
Resposta

 

 

 

 

Bibliografia:

GERD, A. Bornheim. Os filósofos pré-socráticos. São Paulo: Cultrix, 1967.

KIRK, G. S. e RAVEN, J. E. Os filósofos pré-socráticos. 2ª edição. Lisboa: Fundação Calouste Gulbenkian, 1982.

 

Páginas da Internet consultadas:

http://pt.wikipedia.org/wiki/
Imperativo_categ%C3%B3rico

http://pt.wikipedia.org/wiki/
Teorema_das_quatro_cores

http://www.atractor.pt/matviva/
geral/t5cores/T4C.htm

http://www.ime.usp.br/~leo/
imatica/historia/duplica-cubo.html

http://pt.wikipedia.org/wiki/
Duplica%C3%A7%C3%A3o_do_cubo

http://pt.wikipedia.org/wiki/Arquitas_de_Tarento

 

Música de fundo:

Rodia

Fonte:

http://www.navis.gr/midi/midi.htm#Greek