Na
Matemática, os Números de Fibonacci são uma seqüência
definida como recursiva pela fórmula abaixo:
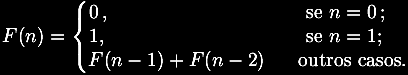
Na
prática, começa-se com 1 e 1, e, então, são
produzidos os próximos números de Fibonacci pela soma dos
dois números anteriores. Só a neutralidade do laissez-faire
e a negligência do
laissez-aller podem ser mais
fáceis do que isto.
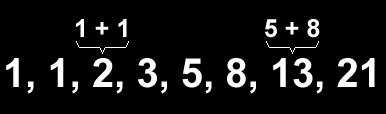
A
Seqüência de Fibonacci foi descrita primeiramente por Leonardo
Pisano ou Leonardo de Pisa (1170 – 1250), também conhecido
como Fibonacci. Em particular, a seqüência de Fibonacci com F(1)
= 1 e F(2) = 3 é conhecida como os números de Lucas (1, 3,
4, 7, 11, 18, 29...). A importância dos números de Lucas L(n)
reside no fato de eles gerarem a Proporção Áurea para
as enésimas potências. Os números de Lucas se relacionam
com os de Fibonacci pela fórmula:
L(n) = F(n - 1) + F(n + 1)
A
proporção áurea, número de ouro, número
áureo ou ainda proporção dourada é uma constante
real algébrica irracional denotada pela letra grega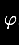 
(phi),
escolhida em homenagem a Phidias, que foi o arquiteto encarregado da construção
do Parthenon. Com valor arredondado a três casas decimais
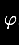é igual a 1,618. É um número irracional (na verdade,
o primeiro número irracional conhecido) que, por ser considerado
por muitos o símbolo da harmonia, há muito tempo é
empregado na arte. Por outros, é considerado o número mais
belo do Universo e uma oferta de Deus ao mundo. A proporção
áurea também é chamada de seção áurea,
razão áurea, razão de ouro, divina proporção,
proporção em extrema razão e divisão de extrema
razão.
Cálculo
do número 
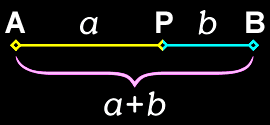
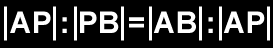
A
razão áurea é definida algebricamente como:
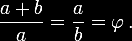
A
equação da direita mostra que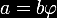 
,
valor que pode ser substituído em a na parte esquerda, resultando
em:
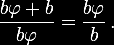
Como
há b demais aí em cima enfeando a equação, todos
eles podem ser cancelados em ambos os lados. E assim, depois da simplificação,
tem-se:
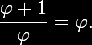
Multiplicando
ambos os lados por ,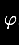
o que não altera nada, mas serve para eliminar o denominador da fração,
resulta:
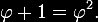
Finalmente,
subtraindo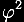 
de ambos os membros
da equação e multiplicando todas as parcelas por - 1, encontramos
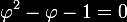, que
é uma equação quadrática da forma ax2
+ bx + c = 0, em que, neste caso, a = 1, b =1 e c =1, restando, tão-só,
resolver essa equação quadrática. Pela Fórmula
de Bháskara:
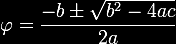
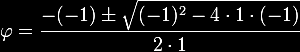
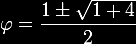
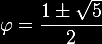
Considerando,
aproximadamente, a raiz quadrada de 5 como sendo 2,236067978, a única
solução positiva desta equação quadrática
é:
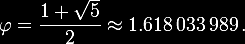
O
Pentagrama
Um
pentagrama regular é obtido traçando-se as diagonais de um
pentágono regular. O pentágono menor, formado pelas interseções
das diagonais, também está em proporção com
o pentágono maior, de onde se originou o pentagrama. A razão
entre as medidas dos lados dos dois pentágonos é igual ao
quadrado da razão áurea. A razão entre as medidas das
áreas dos dois pentágonos é igual a quarta potência
da razão áurea.
Chamando
os vértices de um pentagrama de A, B, C, D e E, o triângulo
isósceles formado por A, C e D tem seus lados em relação
dourada com a base, e o triângulo isósceles A, B e C tem sua
base em relação dourada com os lados.
Quando
Pitágoras descobriu que as proporções no pentagrama
respeitavam a proporção áurea, tornou esse símbolo
estrelado representativo da Irmandade Pitagórica. Este era um dos
motivos que levava Pitágoras a dizer que tudo
é número, ou seja, que a Natureza segue padrões
matemáticos.
Quem
é Deus? Onde está Deus?
Epílogo
Só
faltou dizer uma coisinha: as razões entre um número da Seqüência
de Fibonacci e o que o antecede vão se aproximando do número
de ouro: 1,618. Estas razões variam, um pouco acima, às vezes,
um pouco abaixo, outras vezes, mas a média é 1,618, exatamente,
por exemplo, a proporção das pirâmides do Egito. E,
para não encher de exemplos este epílogo, porque seria necessário
usar como amostra o Universo inteiro, darei apenas um: as proporções
anatômicas dos seres humanos estão todas vinculadas à
proporção áurea e foram bem representadas no Homem
Vitruviano, obra esotérica de Leonardo Da Vinci, mas baseada em uma
famosa passagem do arquiteto romano Marcus Vitruvius Pollio na sua série
de dez livros intitulados De Architectura – um tratado de
arquitetura em que, no terceiro livro, estão descritas as proporções
do corpo humano. Você pode conferir isto com um simples exemplo: meça
a sua altura e depois divida o valor encontrado pelo valor da altura da
depressão cutânea localizada no centro do seu abdome formada
a partir da cicatriz do corte do cordão umbilical (o seu umbigo)
até o chão: o resultado é 1,618. Se não for,
vai correndo a um ortopedista porque, meu irmão, a coisa está
muito esquisita. Mas, antes de ir ao médico, meça tudo de
novo, arredonde aqui e ali, que acaba dando certo. A primeira vez que eu
fiz esse treco achei 3,1416. Quase fiquei louco! Não! Não!
Não! Isto é sacanagem minha.
Homem
Rodolfiano
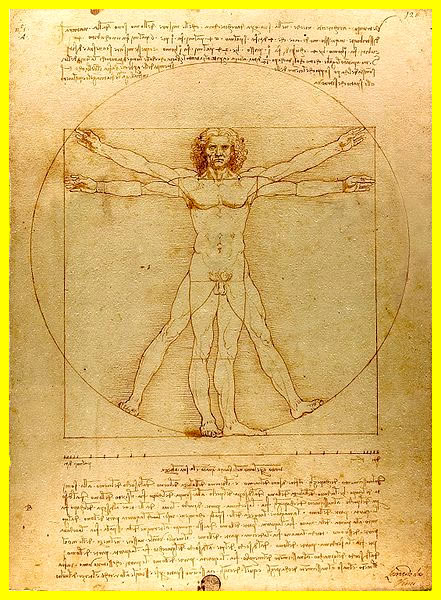
Homem
Vitruviano
Páginas
da Internet consultadas:
http://pt.wikipedia.org/wiki/Homem_Vitruviano
_(desenho_de_Leonardo_da_Vinci)
http://susymcmarques.googlepages.com/
hist%C3%B3riadophi
http://cmup.fc.up.pt/cmup/mecs/O%20
Misterioso%20Numero%20de%20Ouro.pdf
http://pt.wikipedia.org/wiki/Propor
%C3%A7%C3%A3o_%C3%A1urea
http://pt.wikipedia.org/wiki/N%
C3%BAmero_de_Fibonacci
http://pt.wikipedia.org/wiki/
Leonardo_Pisano_Fibonacci
Fundo
musical:
Mona
Lisa
Compositores: Ray Evans & Jay Livingston
Fonte:
http://www.almanaque.cnt.br/
codigodavinci/codigodavinci03.htm